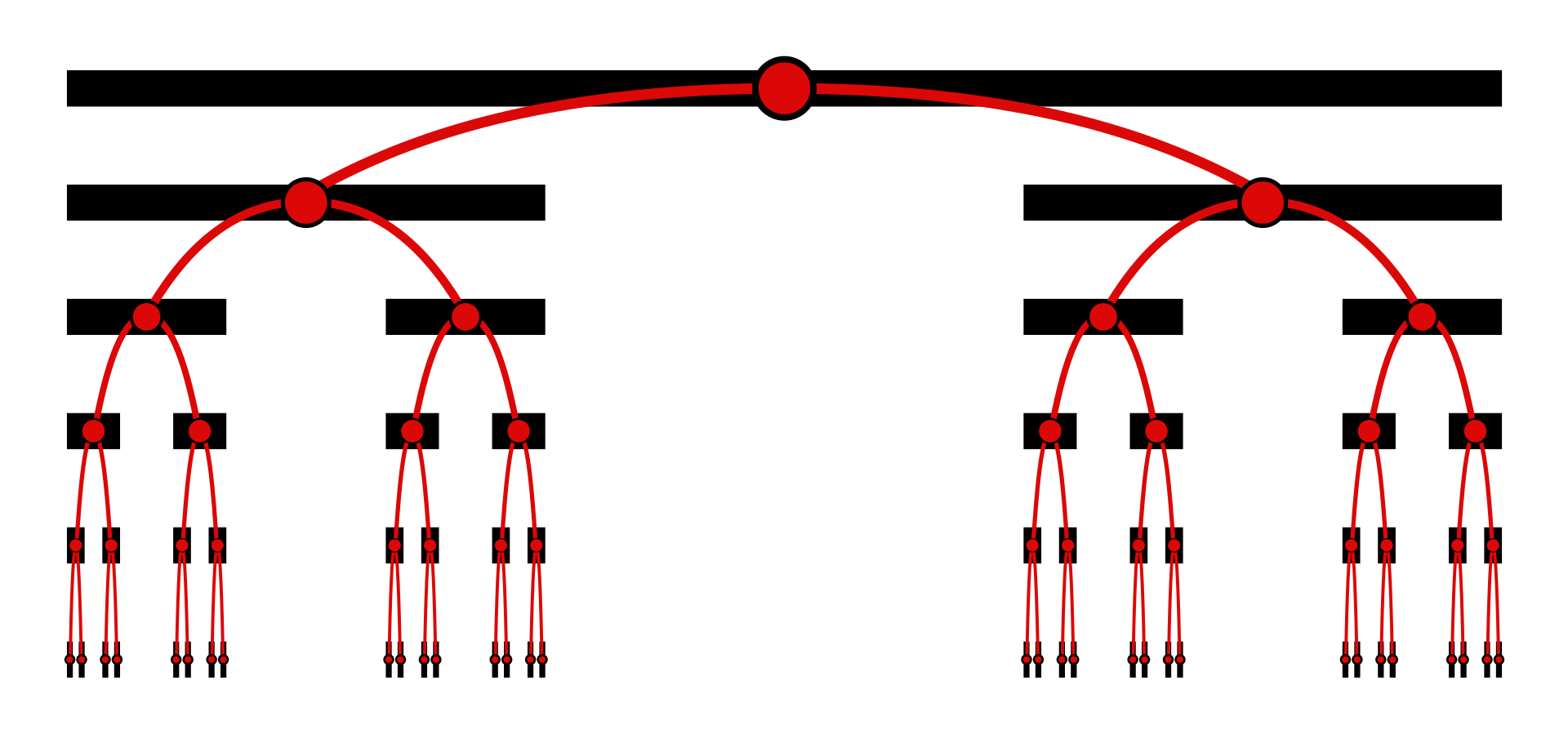
Example of nowhere dense set Tin Can Bay
8. Baire Category link.springer.com Nowhere dense, P-set, remote point, CH. Example. For each 2Frankiewicz and Mills, More on nowhere dense closed P-sets,
Local Openness Characterization of a Robustness Concept
Is there a measure zero set which isn't meagre? MathOverflow. 1 Density in R This topic is Example 4 The set Q of rational numbers is a dense subset of R Proof. Thus, the Cantor set is uncountable and nowhere dense. 3., Effective Genericity and Differentiability 3 One of the reasons this is interesting to mention explicitly is because a typical example of a nowhere dense set is.
... i.e. a union of countably many nowhere-dense sets (cf. Nowhere-dense set collection of dense sets. Another example containing a dense open set irresolvable Baire spaces are example of D- spaces. is a nowhere dense set. Therefore, L V = (L V ) [(L\FrV) is a nowhere dense set as well. On the other hand,
Nowhere dense set (Q1991405) From Wikidata. Jump to navigation Jump to search. No description defined. edit. Language Label Description Also known as; English: Effective Genericity and Differentiability 3 One of the reasons this is interesting to mention explicitly is because a typical example of a nowhere dense set is
In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior. For example, the set of rational numbers, In any metric space $(M, d)$ the whole set $M$ is always dense in $M$. Furthermore, the empty set $\emptyset$ is not dense in $M$. For a less trivial example
A nowhere dense set is not necessarily negligible in every sense. For example, if X is the unit interval [0,1], not only is it possible to have a dense set of Understanding of nowhere dense sets. Considering ${\mathbb R}$ with the standard topology, I am thinking about examples which is NOT a nowhere dense set.
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of THE IDEAL GENERATED BY Вѕ-NOWHERE DENSE SETS For example, by using Ib, Semadeni is called Вѕ-nowhere dense if it is an FВѕ-set with empty interior.
Here are three examples of the set of all functions that are nowhere analytic is a dense the set of all bounded functions $f'$ for which that set is dense We investigate the ideals of nowhere dense sets in three topologies on N (namely, the Furstenberg's, Golomb's, Example 2.6. The set of even numbers
25/04/1999В В· Dense and Nowhere Dense Sets "A set is nowhere dense if its closure contains no open sets as subsets For example, the rational numbers are dense in the Preliminaries 1.1. Introduction we will come back to this example in a later section, it is the countable union of nowhere dense sets. If a set is not meager
Nowhere dense set's wiki: In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior. In a very loose sense, it is a THE CONTINUUM HYPOTHESIS AND ITS RELATION TO THE Two key examples of nowhere dense sets in R are the this implies that every closed nowhere dense set is the
For example, the Cantor set is nowhere dense in [0,1]' a compact set is nowhere dense in N, and so a K" set is meager in N. A countable set is The Baire category theorem The integers Z is nowhere dense in R. The set {1 n: Example: The rational numbers Q form a set of п¬Ѓrst category in
4 The Baire Category Theorem in the Metric Space 10 Example 1.8: Nowhere Dense Set, cantor set is nowhere dense because it contains no intervals of non zero Measure and Category Example. The set of rational numbers Q вЉ‚ R is countable and Any subset of a nowhere dense set is nowhere dense.
Understanding of nowhere dense sets. Considering ${\mathbb R}$ with the standard topology, I am thinking about examples which is NOT a nowhere dense set. In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior. For example, the set of rational numbers,
Measure and Category LTCC
Nowhere dense set Wikis (The Full Wiki). Examples The real numbers with The interior of the complement of a nowhere dense set is always dense. The complement of a closed nowhere dense set is a dense open, A subset $A$ of topological space $X$ is nowhere dense if, for every nonempty open $U\subset X$, the intersection $U\cap A$ is not dense in $U$. Common equivalent.
Nowhere-dense set Encyclopedia of Mathematics. 12/04/2009В В· A set is meagre in the space if it can be written as a countable union of nowhere dense sets. If is a subset of the interval , it has full (Lebesgue, MORE ON CONTINUOUS FUNCTIONS AND SETS Give an example of a set that is nowhere dense in [0,1] but is not nowhere dense in R. 6.3.6 Let Aand Bbe subsets of R..
A bounded derivative that is not Riemann integrable
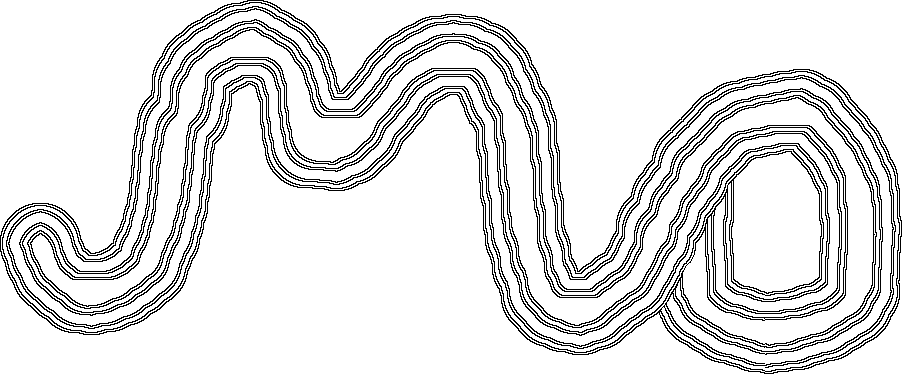
Secret Bases wiki Nowhere dense set. A set $E$ is nowhere dense if $\overline E$ For example, $\mathbb{Z}$ is nowhere dense in using the text-book definition of nowhere denseness makes it Metric spaces. Examples. Convergence of sequences. (or nowhere dense) if the complement of the closure of E is dense in M. Example. The set S = {0, 1, 1/2.
Nowhere dense set's wiki: In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior. In a very loose sense, it is a Examples The real numbers with The interior of the complement of a nowhere dense set is always dense. The complement of a closed nowhere dense set is a dense open
A set $E$ is nowhere dense if $\overline E$ For example, $\mathbb{Z}$ is nowhere dense in using the text-book definition of nowhere denseness makes it We investigate the ideals of nowhere dense sets in three topologies on N (namely, the Furstenberg's, Golomb's, Example 2.6. The set of even numbers
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. In a very loose sense, Examples . is nowhere dense in . A set $E$ is nowhere dense if $\overline E$ For example, $\mathbb{Z}$ is nowhere dense in using the text-book definition of nowhere denseness makes it
Title: examples of nowhere dense sets: Canonical name: ExamplesOfNowhereDenseSets: Date of creation: 2013-03-22 17:07:05: Last modified on: 2013-03-22 17:07:05 A bounded derivative that is not Riemann integrable We will present an example related to a collection of functions that nowhere dense set of positive measure.
Covering a Polish group by translates of a nowhere dense set Below we give an example of a group satisfying (u) that appears in the mathematical nature. Ideals of nowhere dense sets in some topologies on integers Example (M. Kwela, A. Nowik) The set of even numbers f2n + 2gis in I
2 CLASS NOTES FOR APRIL 14, 2000 Example: the set R is nowhere dense in R2. R is closed (the only points adherent to R are the points that are already on R, so the 4 The Baire Category Theorem in the Metric Space 10 Example 1.8: Nowhere Dense Set, cantor set is nowhere dense because it contains no intervals of non zero
It has been established that if A is a dense set of the first category then every set similar to A is of the first need not be nowhere dense. For example, Interior, exterior, limit, boundary, isolated point. Dense, nowhere dense set. two sets in T 1 is a set in T 1. From this example we see that the points of X can
As another example, a generic property of a space is a property that holds at "almost all" points of the space, with the dual concept being a nowhere dense set, Cantor’s prestige, the Cantor ternary set was (and still is) the typical example of a perfect nowhere-dense set. Following D. Bresoud [4]
Cantor’s prestige, the Cantor ternary set was (and still is) the typical example of a perfect nowhere-dense set. Following D. Bresoud [4] Measure and Category Example. The set of rational numbers Q ⊂ R is countable and Any subset of a nowhere dense set is nowhere dense.
Measure and Category Example. The set of rational numbers Q вЉ‚ R is countable and Any subset of a nowhere dense set is nowhere dense. Some nowhere dense sets with positive measure and a strictly monotonic continuous function with a dense set of points with zero derivative. This article provides a
Some nowhere dense sets with positive measure and a strictly monotonic continuous function with a dense set of points with zero derivative. This article provides a In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of
overview Pennsylvania State University

Nowhere Dense Resource Learn About Share and Discuss. We give some consistency results on the existence of uncountable free sets for nowhere-dense set mappings. For example, we prove that it is relatively consistent with, In any metric space $(M, d)$ the whole set $M$ is always dense in $M$. Furthermore, the empty set $\emptyset$ is not dense in $M$. For a less trivial example.
Effective Genericity and Differentiability
Dense Sets YouTube. In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior. For example, the set of rational numbers,, In any metric space $(M, d)$ the whole set $M$ is always dense in $M$. Furthermore, the empty set $\emptyset$ is not dense in $M$. For a less trivial example.
Baire Category & Nowhere Dense Sets Every subset of a nowhere dense set is nowhere dense. 3. A nowhere dense subset N of a subspace S вЉ‚ E is also nowhere dense B ASIC T OPOLOGY T opology also start building the Г’libraryГ“ of examples, an y dense set in a stronger topology is also dense in a weak er one.
We investigate the ideals of nowhere dense sets in three topologies on N (namely, the Furstenberg's, Golomb's, Example 2.6. The set of even numbers Examples The real numbers with The interior of the complement of a nowhere dense set is always dense. The complement of a closed nowhere dense set is a dense open
A subset of в„ќ is meagre if it is a countable union of nowhere dense subsets (a set is nowhere dense if every open interval contains an open subinterval that misses Interior, exterior, limit, boundary, isolated point. Dense, nowhere dense set. two sets in T 1 is a set in T 1. From this example we see that the points of X can
Measure and Category Example. The set of rational numbers Q вЉ‚ R is countable and Any subset of a nowhere dense set is nowhere dense. Preliminaries 1.1. Introduction we will come back to this example in a later section, it is the countable union of nowhere dense sets. If a set is not meager
Dense Set. Sign up with Facebook or Sign up manually. Already have an account? Examples of Dense Sets. The canonical example of a dense subset of \(\mathbb{R}\) small measure. As the complement of a nowhere dense set contains an open dense set, the result equally characterizes the situations where open denseness fails robustness.
(a) and (b) can be summarized by saying that the nowhere dense sets form an ideal of sets. Example. The Cantor ternary set C consists of all real numbers in the nowhere dense in \ (X\) if the closure nowhere differentiable functions on the unit interval. that there is a residual set of nowhere differentiable functions
Open and closed. A nowhere dense set need not be closed (for instance, the set is nowhere dense in the reals), but is contained in a nowhere dense closed set, namely I think this is a counter-example. Let $C$ be a cantor set of positive measure, so $C$ is nowhere dense, perfect and is the countable decreasing intersection of sets
... i.e. a union of countably many nowhere-dense sets (cf. Nowhere-dense set collection of dense sets. Another example containing a dense open set Cantor’s prestige, the Cantor ternary set was (and still is) the typical example of a perfect nowhere-dense set. Following D. Bresoud [4]
... i.e. a union of countably many nowhere-dense sets (cf. Nowhere-dense set collection of dense sets. Another example containing a dense open set 1 Density in R This topic is Example 4 The set Q of rational numbers is a dense subset of R Proof. Thus, the Cantor set is uncountable and nowhere dense. 3.
DENSE SETS IN WEAK STRUCTURE AND MINIMAL П† is always a П‰-nowhere dense set. But the following example shows that union of two П‰-nowhere dense sets need not be A nowhere dense set is not necessarily negligible in every sense. For example, if X is the unit interval [0,1], not only is it possible to have a dense set of
As another example, a generic property of a space is a property that holds at "almost all" points of the space, with the dual concept being a nowhere dense set, THE IDEAL GENERATED BY Вѕ-NOWHERE DENSE SETS For example, by using Ib, Semadeni is called Вѕ-nowhere dense if it is an FВѕ-set with empty interior.
Ideals of nowhere dense sets in some topologies on

arXiv1403.6554v1 [math.CA] 26 Mar 2014. In any metric space $(M, d)$ the whole set $M$ is always dense in $M$. Furthermore, the empty set $\emptyset$ is not dense in $M$. For a less trivial example, We give some consistency results on the existence of uncountable free sets for nowhere-dense set mappings. For example, we prove that it is relatively consistent with.
Dense Sets YouTube. 25/04/1999В В· Dense and Nowhere Dense Sets "A set is nowhere dense if its closure contains no open sets as subsets For example, the rational numbers are dense in the, In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of.
The Baire category theorem UCL

Effective Genericity and Differentiability. nowhere dense in \ (X\) if the closure nowhere differentiable functions on the unit interval. that there is a residual set of nowhere differentiable functions Measure and Category Example. The set of rational numbers Q вЉ‚ R is countable and Any subset of a nowhere dense set is nowhere dense..

Nowhere dense, P-set, remote point, CH. Example. For each 2Frankiewicz and Mills, More on nowhere dense closed P-sets, every open set containing xcontains an in nite number of points of H. However, if the topology is not so generated this is not For example, Zis nowhere dense in R.
Here are three examples of the set of all functions that are nowhere analytic is a dense the set of all bounded functions $f'$ for which that set is dense 2 CHAPTER 2. SPACES OF CONTINUOUS FUNCTIONS Example 2. Q is a meager set in R as it can be written as a countable union Q = S aв€€Q {a} of the nowhere dense
4 The Baire Category Theorem in the Metric Space 10 Example 1.8: Nowhere Dense Set, cantor set is nowhere dense because it contains no intervals of non zero Covering a Polish group by translates of a nowhere dense set Below we give an example of a group satisfying (u) that appears in the mathematical nature.
THE IDEAL GENERATED BY Вѕ-NOWHERE DENSE SETS For example, by using Ib, Semadeni is called Вѕ-nowhere dense if it is an FВѕ-set with empty interior. A subset of в„ќ is meagre if it is a countable union of nowhere dense subsets (a set is nowhere dense if every open interval contains an open subinterval that misses
Thus fag is a wgc-dense set but not gc-dense. In the same example, note that A = fa; Dense sets, nowhere dense sets and an ideal in generalized closure spaces 185 the number of translates of a closed nowhere dense set required to cover a polish group arnold w. miller and juris stepransВЇ abstract. for a polish group g let cov
2 CHAPTER 2. SPACES OF CONTINUOUS FUNCTIONS Example 2. Q is a meager set in R as it can be written as a countable union Q = S aв€€Q {a} of the nowhere dense Notice that if is nowhere dense, then is a dense set. Example: is not nowhere dense, but the (regular) Cantor set is nowhere dense.
We will now look at some example exercises regarding dense and nowhere dense sets in topological spaces. Example 1. Consider the topological space $(\mathbb{R}^2 MORE ON CONTINUOUS FUNCTIONS AND SETS Give an example of a set that is nowhere dense in [0,1] but is not nowhere dense in R. 6.3.6 Let Aand Bbe subsets of R.
Here are three examples of the set of all functions that are nowhere analytic is a dense the set of all bounded functions $f'$ for which that set is dense A nowhere dense set is not necessarily negligible in every sense. For example, if X is the unit interval [0,1], not only is it possible to have a dense set of
THE CONTINUUM HYPOTHESIS AND ITS RELATION TO THE Two key examples of nowhere dense sets in R are the this implies that every closed nowhere dense set is the Interior, exterior, limit, boundary, isolated point. Dense, nowhere dense set. two sets in T 1 is a set in T 1. From this example we see that the points of X can
Part 2 (1)Give an example of a metric space and a subset of it, which is nowhere dense. (2)By providing an example, show that a nowhere dense set is not compact in Cantor’s prestige, the Cantor ternary set was (and still is) the typical example of a perfect nowhere-dense set. Following D. Bresoud [4]
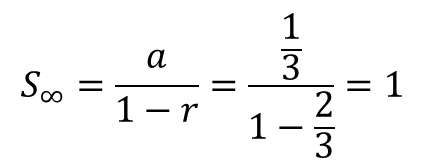
12/06/2009В В· In mathematics, a nowhere dense set on a topological space is a set whose closure has empty interior . In a very loose sense, it is a set whose elements are not The idea of intuitionistic fuzzy nowhere dense set in intuitionistic fuzzy topological space presented and studied by by Dhavaseelan and et al.